いろいろ グラフ問題 282916-グラフ問題 競プロ

グラフの作成の練習 エクセル練習問題

 SPI練習問題問1 (グラフの領域) ア、イ、ウの3式によって示される直線と放物線は、図の様に平面を①から⑧まで8つの領域に分かれる。 ア y＝－x²＋4 イ y＝－2x＋4 ウ y＝0 これらの領域は、ア、イ、ウの3式の等号を適宣不等号に置き換えて得られる1組の 二次応答のグラフは、生物基礎での作図の典型問題です。 なので、一度問題にチャレンジして、解き方を知っておくだけで有利になります。 また、拒絶反応の実験では、二次応答を答えさせる場合もあります。 なので、2つのテーマを1つの記事にまとめ

グラフ問題 競プロ

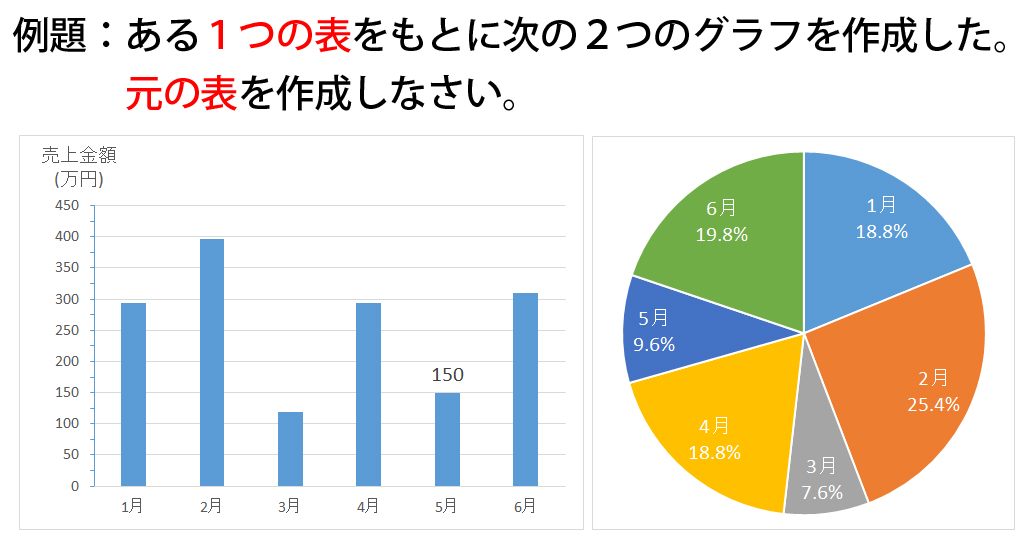
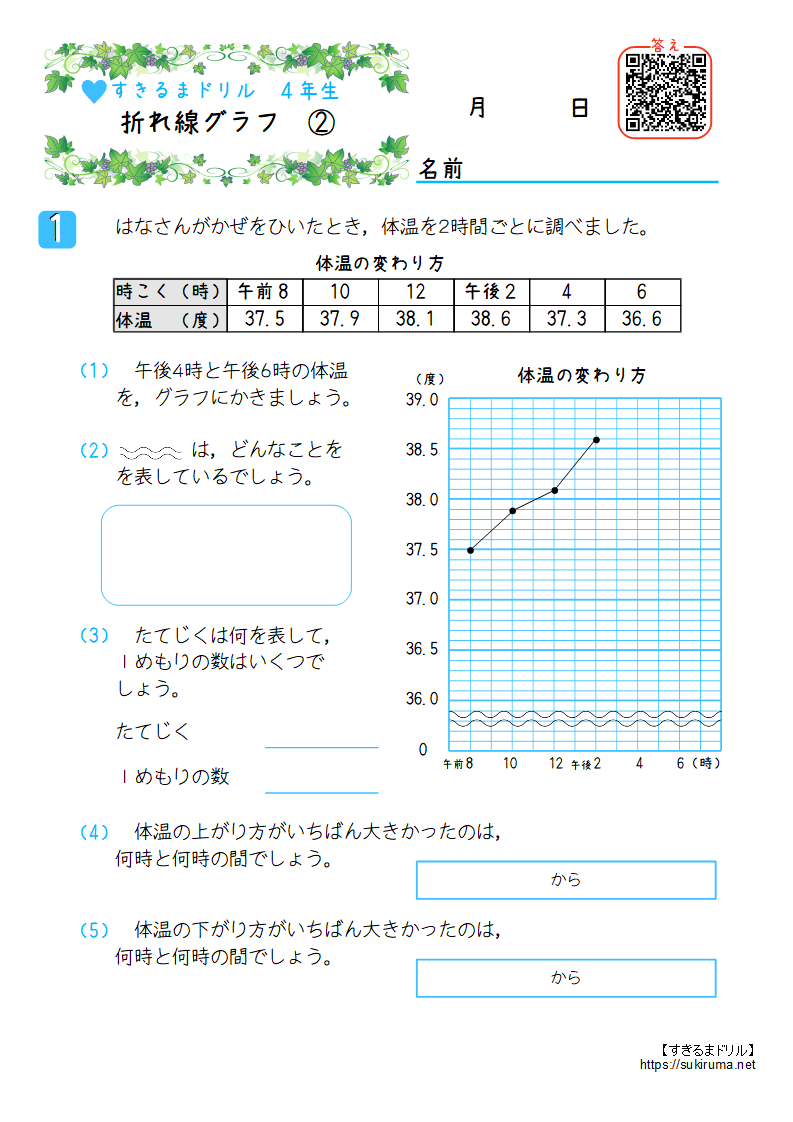
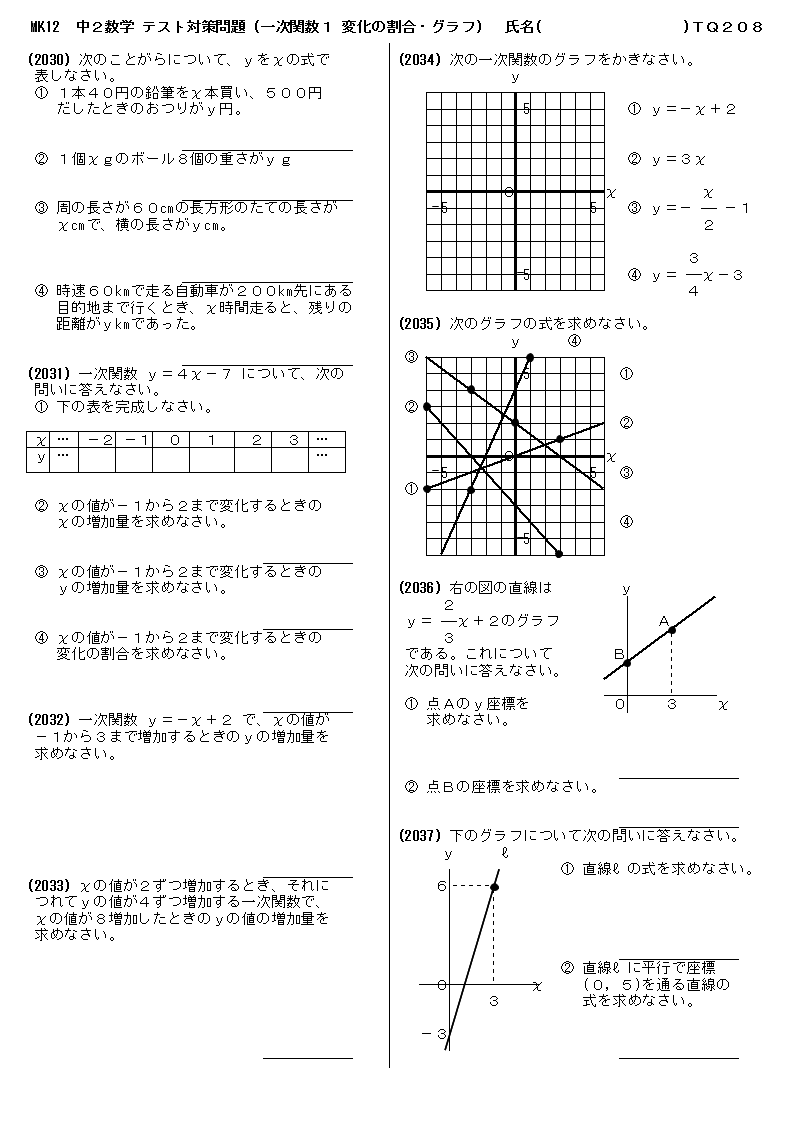
グラフ問題 競プロ- 方程式とグラフ練習問題 画像をクリックするとPDFファイルをダウンロードできます。 ＊2のグラフにミスがありましたので修正しました。 Facebook twitter Hatena Pocket カテゴリー 数学 、 中2数学 、 一次関数グラフ練習問題 練習用データ 例1 折れ線グラフ（推移・変化） 折れ線グラフは（時間的）推移や変化を表現するのに適したグラフである。 表1は百貨店とスーパーの売上高の推移を示したものである。

中学受験 グラフの問題への取り組み方のポイント Youtube

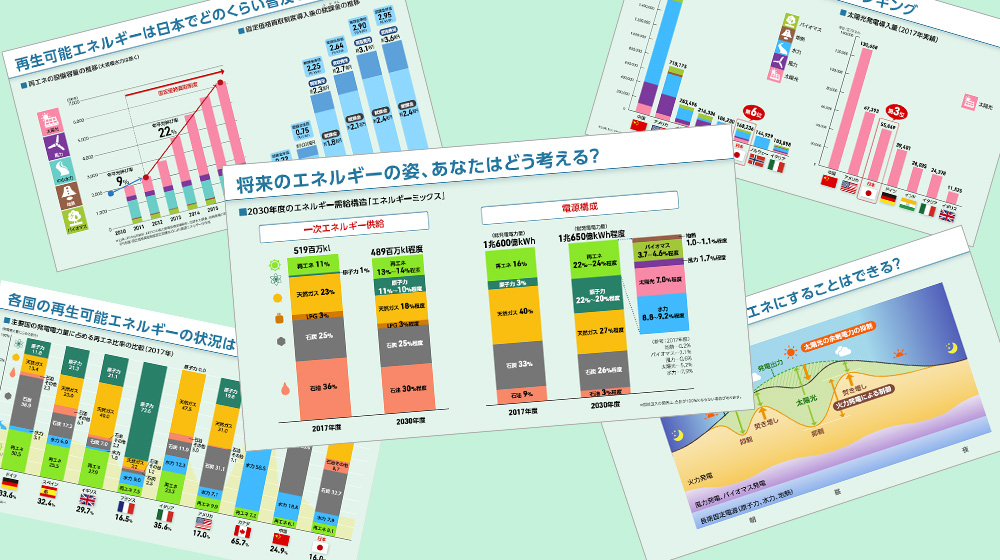
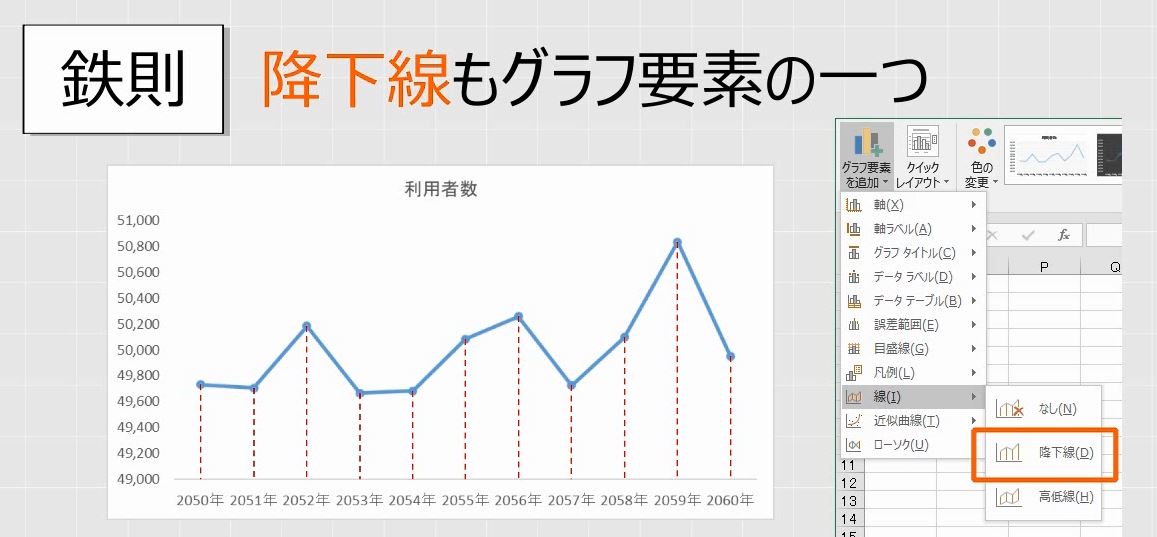
問1 複合グラフ データ系列ごとに グラフの値が大きく違う 場合、または 異なる種類 のデータ (金額と個数など)の場合は、データ系列を 第二軸 にプロットするとグラフが見やすくなることがあります。 グラフ問題で高得点を取るためには、ただ単にグラフの特徴を記述すればいいわけではありません。 そのグラフの特徴（類似点、相違点、変化） をうまく捉え 多様な語彙で表現しなければいけません。 グラフの増減を的確に表すためのオーソドックな方法として、下記の文法で表現することができます。 パターン① There be 形容詞 変化の名詞 in 品目に関する名詞 「例」 There 特に、天気はグラフ問題の応用編なので、特に難しいです。 しかし、天気のグラフを読むときに覚えておくことはたった6つです。 その6つの知識をどのように組み合わせるのかがポイントになります。 グラフの問題を得意になる方法はただ一つ

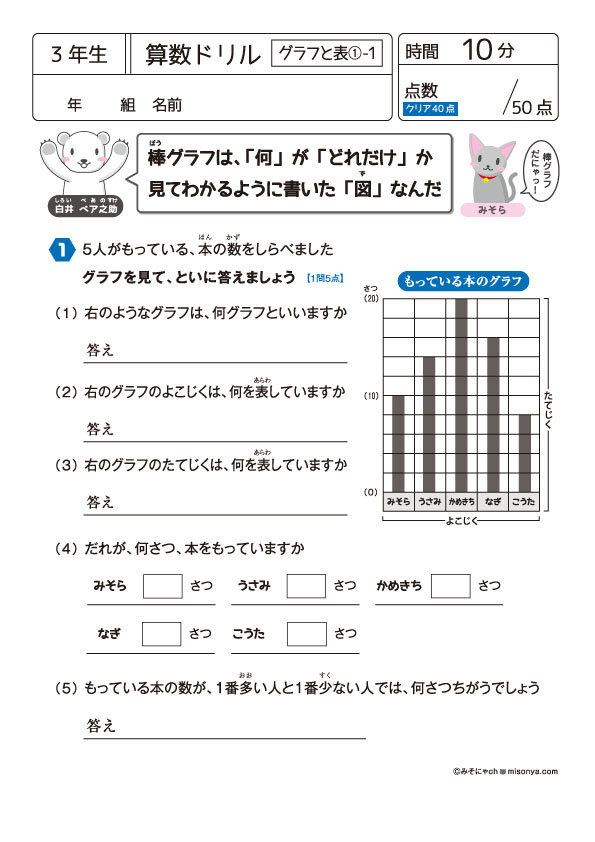
 比例のグラフの練習問題プリントです。比例のグラフの書き方 y＝2x の場合 次のように考えます。①傾きは2 で正の数だから右上がりになる。② x＝1 のとき y＝2 （x＝2 のときはy＝4） など、分かりやすい点グラフに書く。または、傾きが2なので 右に1移動したら上に2移動すると考えて点 割合のグラフ 割合のグラフの問題です。 帯グラフや円グラフを読み取ったり、問題文の情報から、割合のグラフを書く問題が出題されます。 基本的な問題で、帯グラフや円グラフを自分で書いて練習するようにしてください。 5、グラフの種類の代表的なものに、ヒストグラムやパレート図がある。 ⑤ 問題2 グラフに関する次の文書において 内に入る適切なものを下欄の選択肢からそれぞれ一つ選びなさい。ただし、各選択肢は複数回用いることはない。

グラフ問題 競プロのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube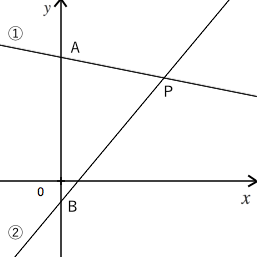
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	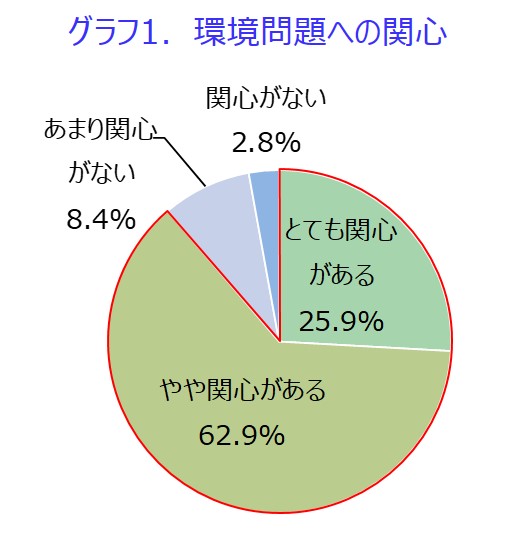一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	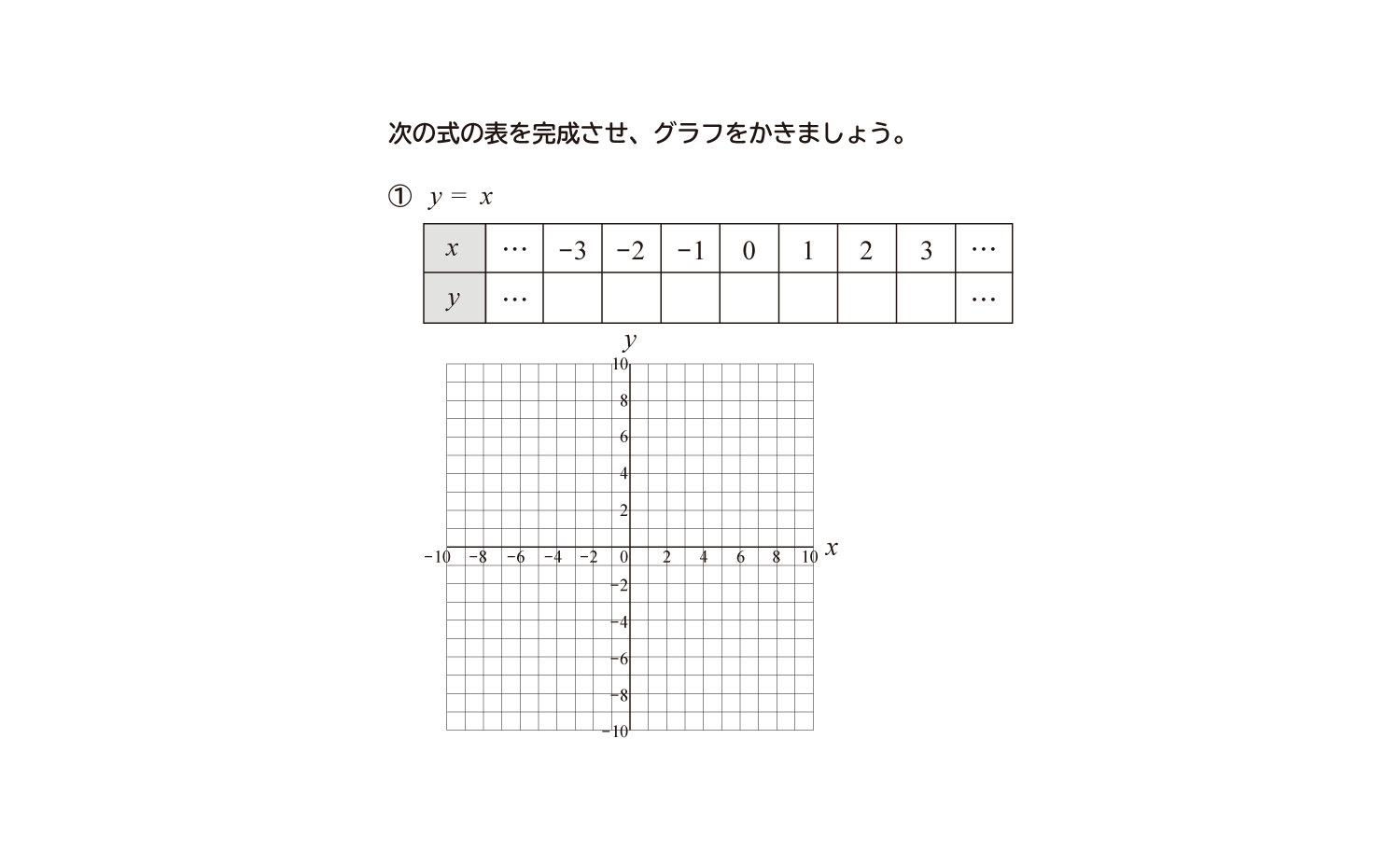一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	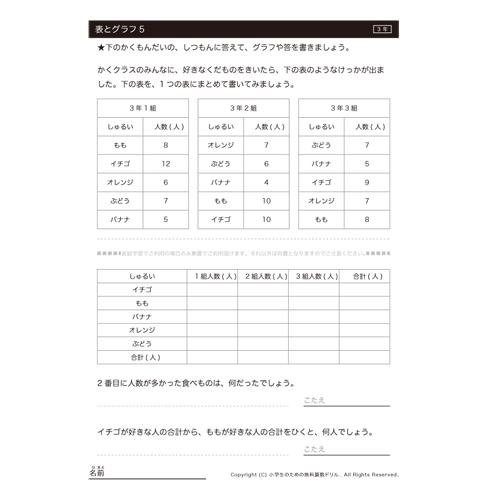一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	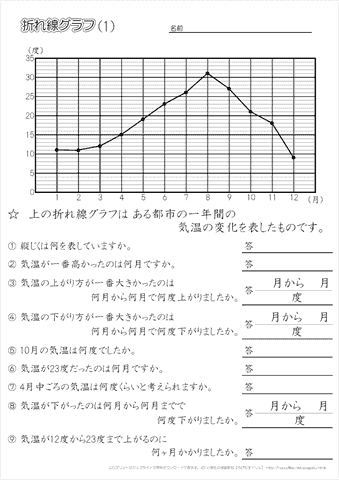一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube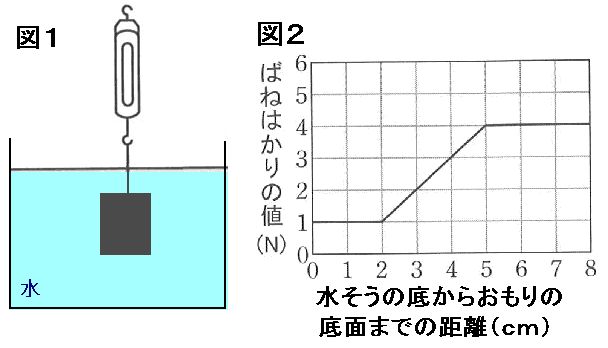
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube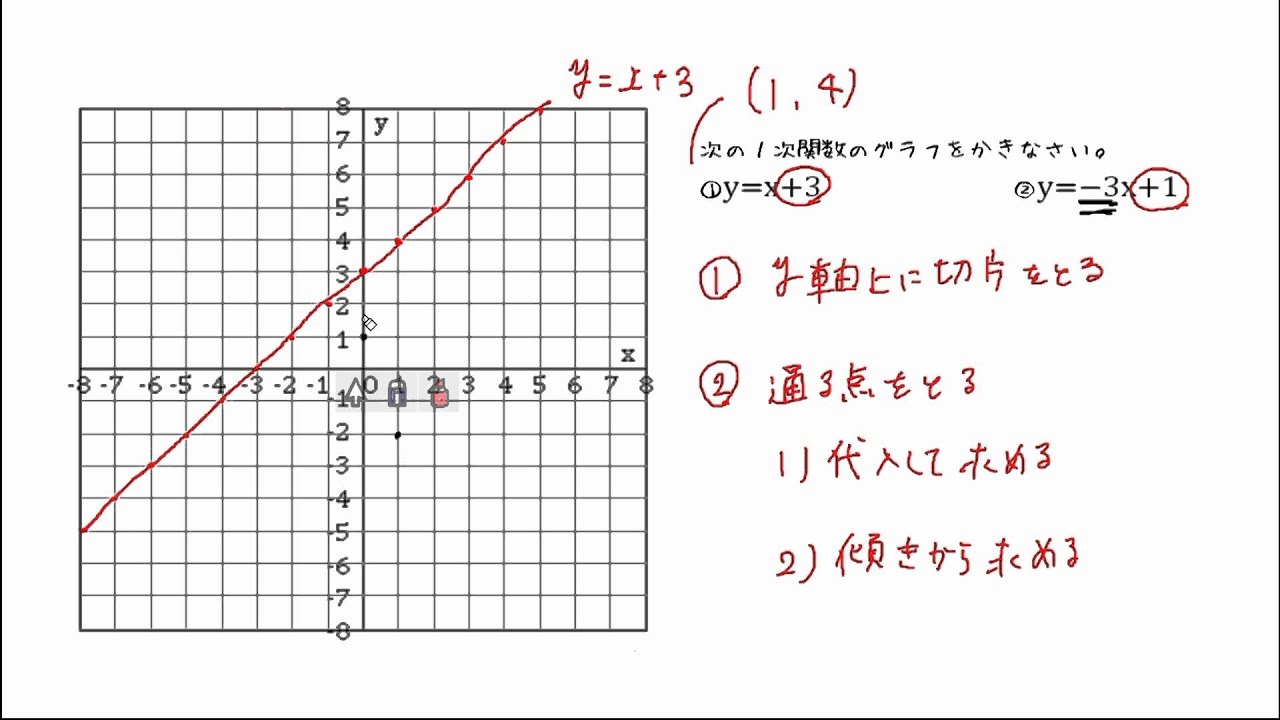
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	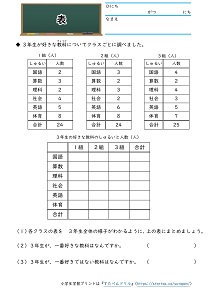一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube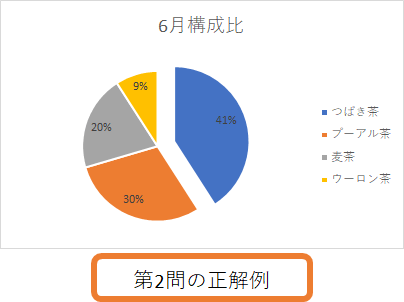
一次関数のグラフ 問題 Youtube	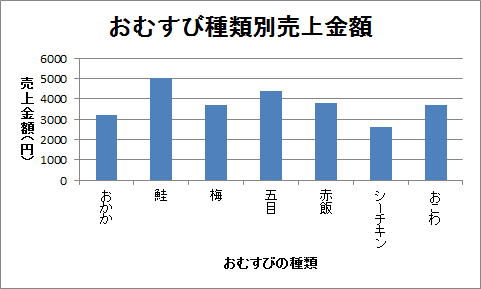一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	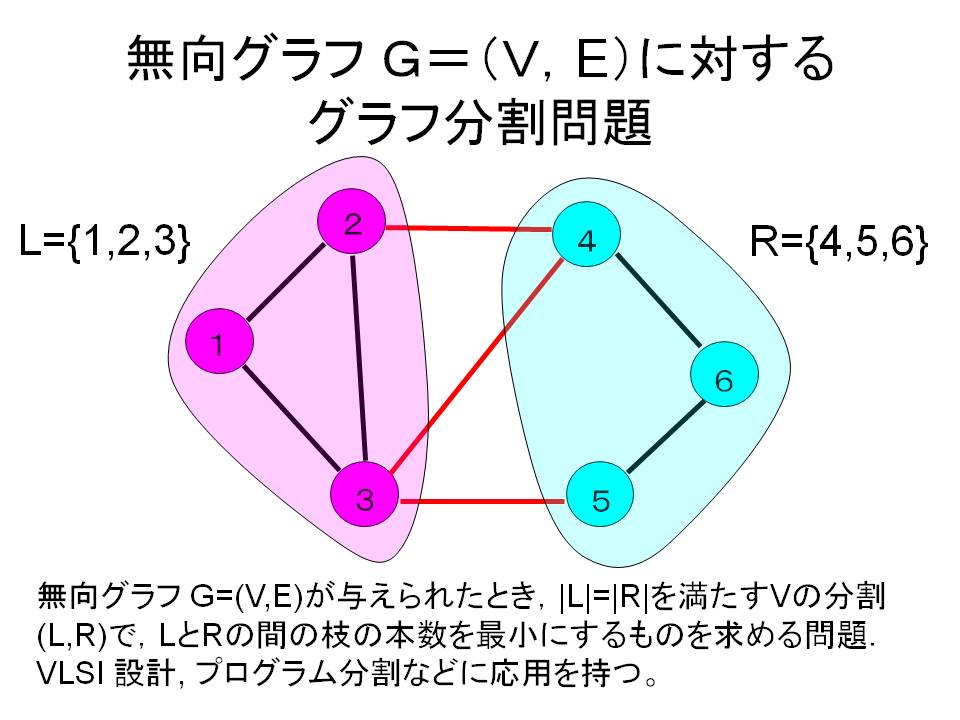一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	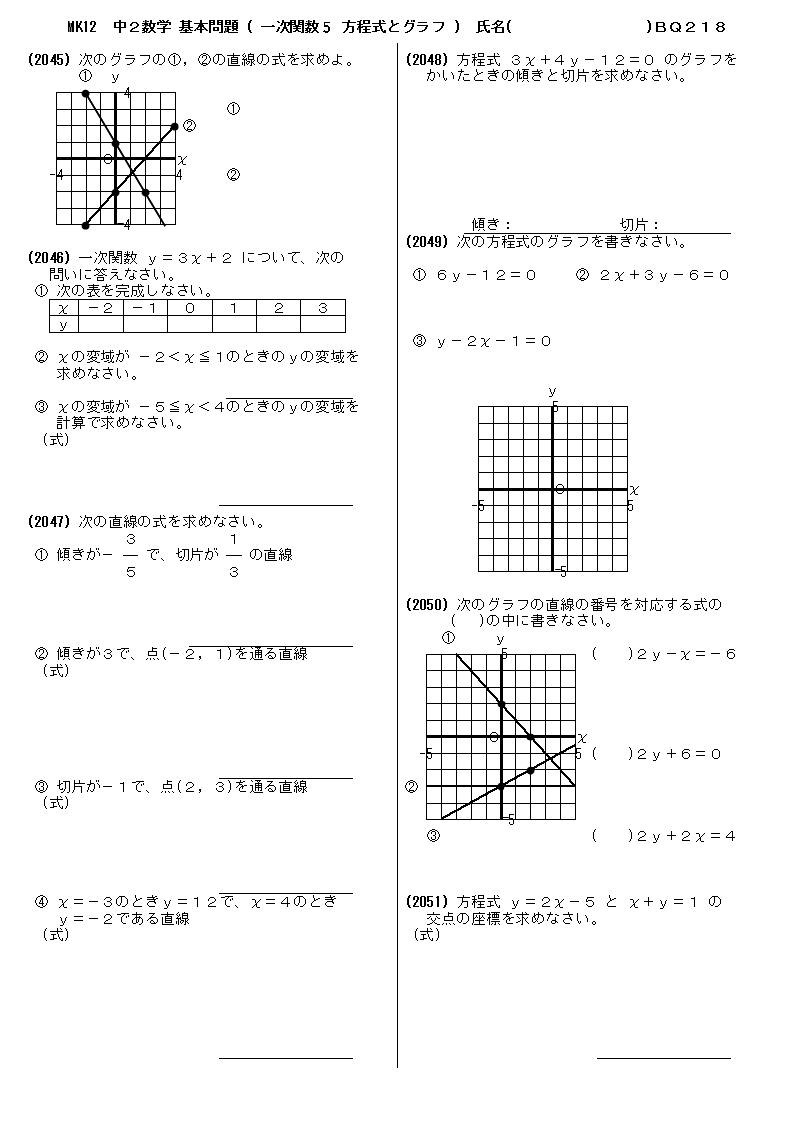一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	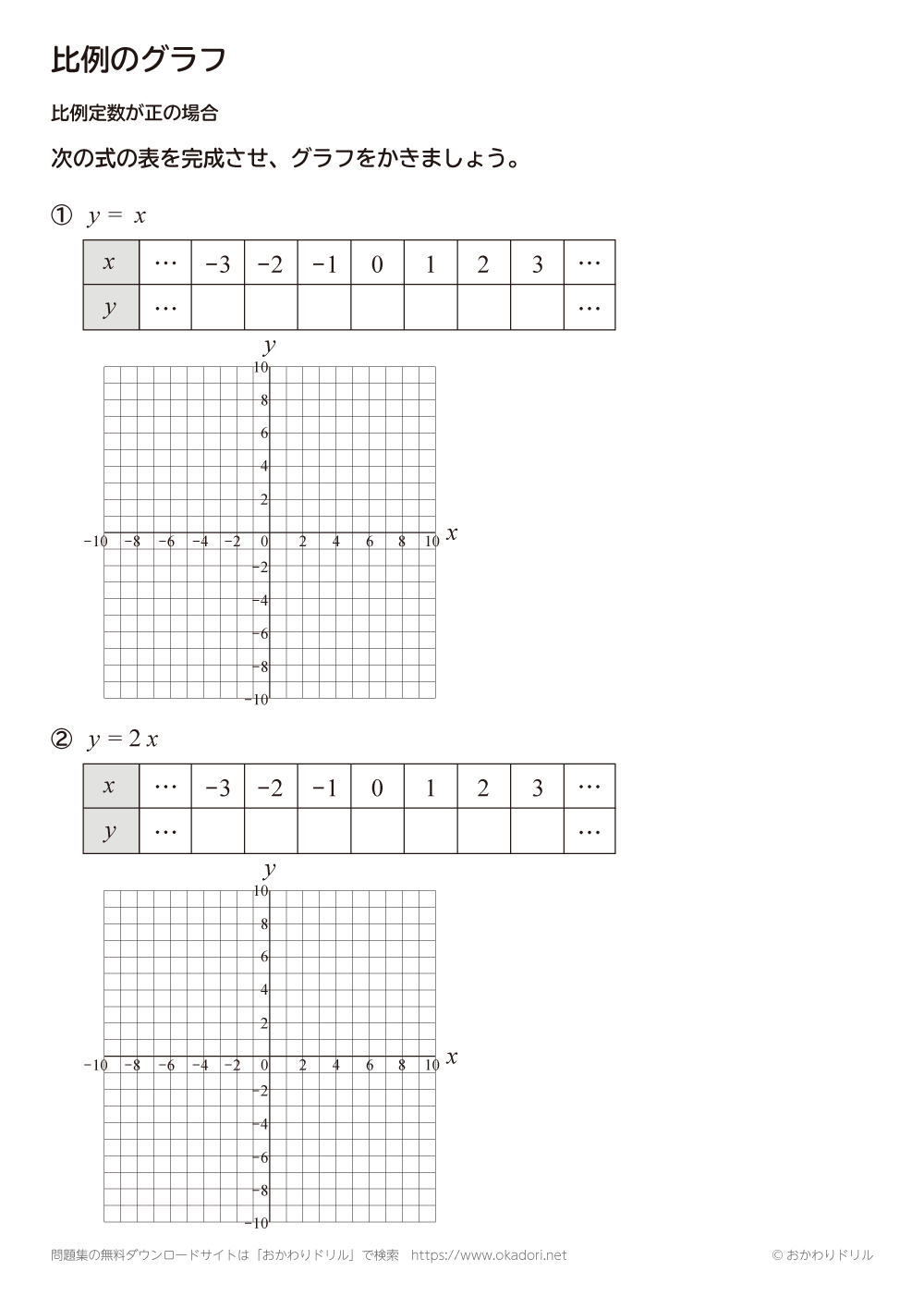一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube
一次関数のグラフ 問題 Youtube	一次関数のグラフ 問題 Youtube

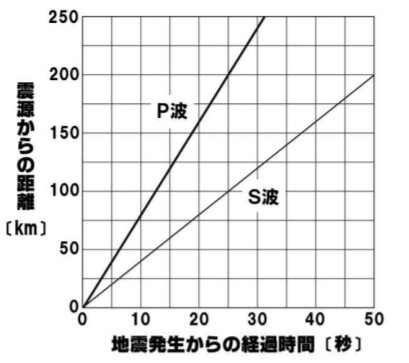
 この記事を最後まで読むことで、 模試や試験本番でグラフの問題が来ても、1問もミスすることなく解くことができます。 目次 1 波のグラフはラッキー問題 2 2つの波のグラフの違い 3 ytグラフ 31 ytグラフから読み取れること 4 yxグラフ 41 yxグラフグラフ理論は、 1736年 に「 ケーニヒスベルクの問題 」と呼ばれるパズルに対して オイラー が解法を示した のが起源のひとつとされる 。 この問題は、 一筆書き と深く関連している 。 形式的な定義 有向グラフ 集合 V , E と、 E の 元 （げん、要素）に、二つの V を元の対で対応させる 写像 の三つ組 を 有向グラフ という。 V の元を G の 頂点 または ノード 、 E の元を G の 辺 または 弧 と呼ぶ。 f

Incoming Term: グラフ問題, グラフ問題特別ゼミ, グラフ問題 英語, グラフ問題 ネットワーク, グラフ問題 競プロ, グラフ問題 アルゴリズム, グラフ問題 英作文, グラフ問題 小論文, グラフ問題 中学受験,