In Real Open Source You Have The Right To Control Your Own Destiny Upupming 的博客
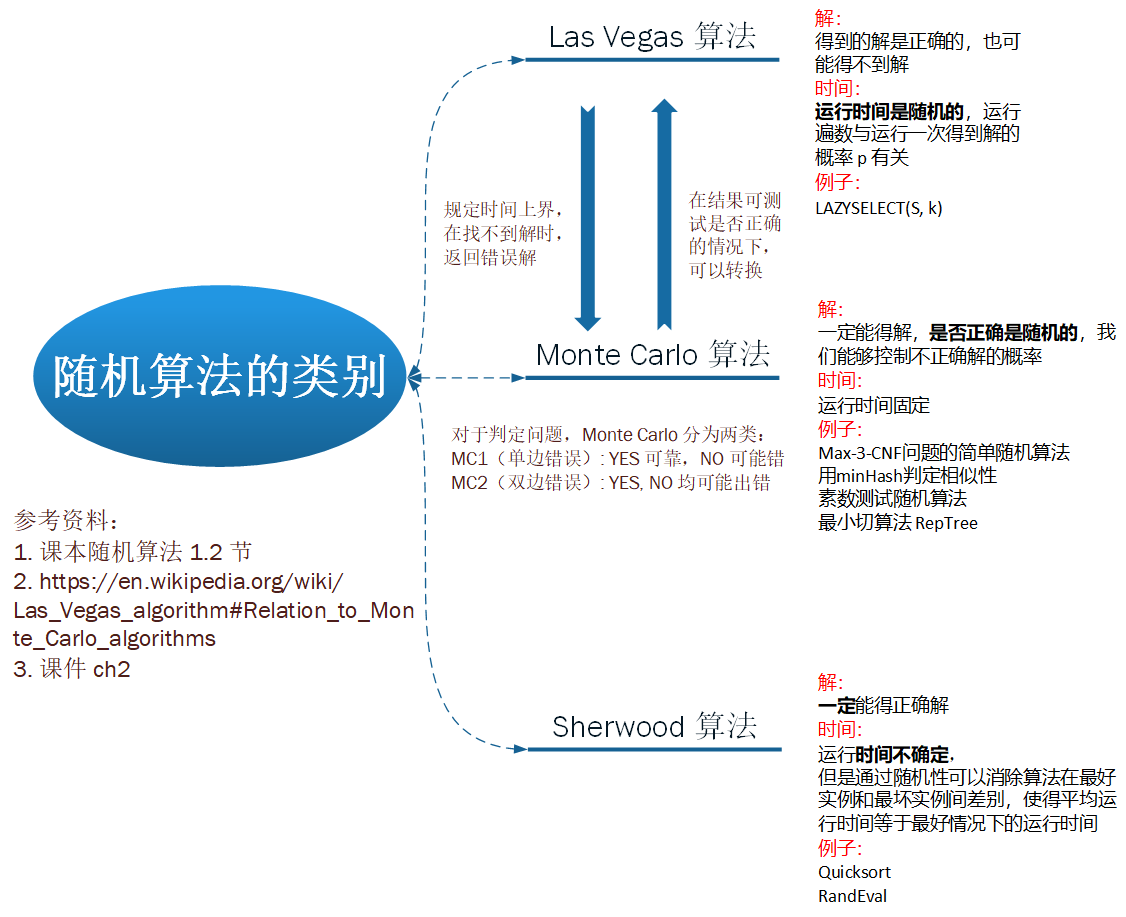
この不等式を満たす\(x\)の変域を求めるのが、指数不等式の問題です。 指数不等式は 指数方程式とほとんど同じ考え方で解きます。 指数方程式が不安な方は先にこちらの記事をご覧ください。 対数不等式 とは, log 2 (x 3) < 2 log 2 (x 1) \log_2 (x3) < 2 \log_2 (x1) lo g 2 (x 3) < 2 lo g 2 (x 1) のように対数(ログ)を含む不等式のことです。 この記事では,対数不等式
不等式 問題 難しい
不等式 問題 難しい- 数と式 一次不等式とは? 解き方や応用問題(文章題、絶対値や分数) 21年11月5日 この記事では「一次不等式」について、式変形による解き方、またグラフを用いた解き方をでき 一次不等式のよくある応用問題+解き方まとめ文章題の攻略法あり 本日の授業内容 「計算問題」編 「xの値の範囲を求めよ」編 「絶対値を含む不等式」編 「連立一次不等式」編

تويتر Yue Zhangyue1977
大学受験の数学ⅡとⅢの不等式の証明問題が誰でも理解できる記事 19年12月16日 22年09月15日 「不等式の証明ができたりできなかったりでやり方がわからないな〜」といっこのことから、"86≦x≦95"に含まれる正の整数の最大値が答えとなります。 答えはそう、9個です。 求める値をxとおく 文章通りに式をたてていく ・ 不等式の移項~足し算と引き算~ ・ 1次不等 難関大の不等式の問題 難関大の不等式の問題の解答 問題1 \(a>0\)とします。不等式\(lx-al<b\)を満たす全ての実数\(x\)に対して、\(lx^2-a^2l<1/2\)が成立するとき、正の数\(b\)は
三角比の頻出問題を総ざらい! 学年末試験が近づいてきました。 この記事では、三角比関連の頻出問題、特に方程式・不等式あたりをご紹介していきます。 試験対策として、ここで説今回は高校数学Ⅰで学習する 「不等式の解き方」 について徹底解説していくよ! 不等式と言っても 連立不等式、絶対値の不等式、文字を含む不等式、二次不等式 このようにバリエーションは 問題 (問題) どんな正の数\(x,y\)に対しても不等式\((xy)^4 \leq c^3 (x^4y^4)\)が成り立つような\(c\)の範囲を求めよ (97 お茶の水女子大学・理学部) 方針 この手の不等式を見た
不等式 問題 難しいのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | 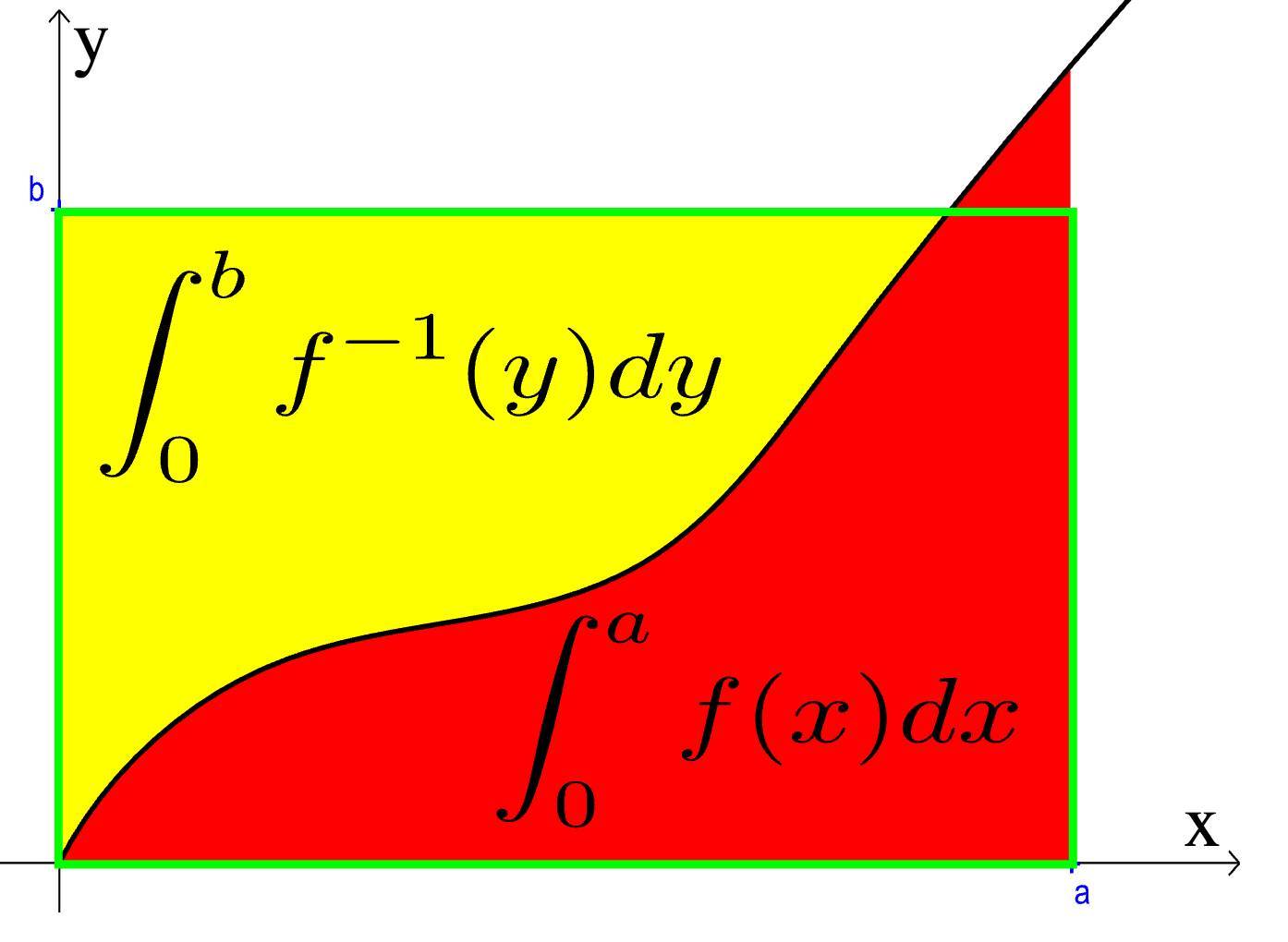 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | 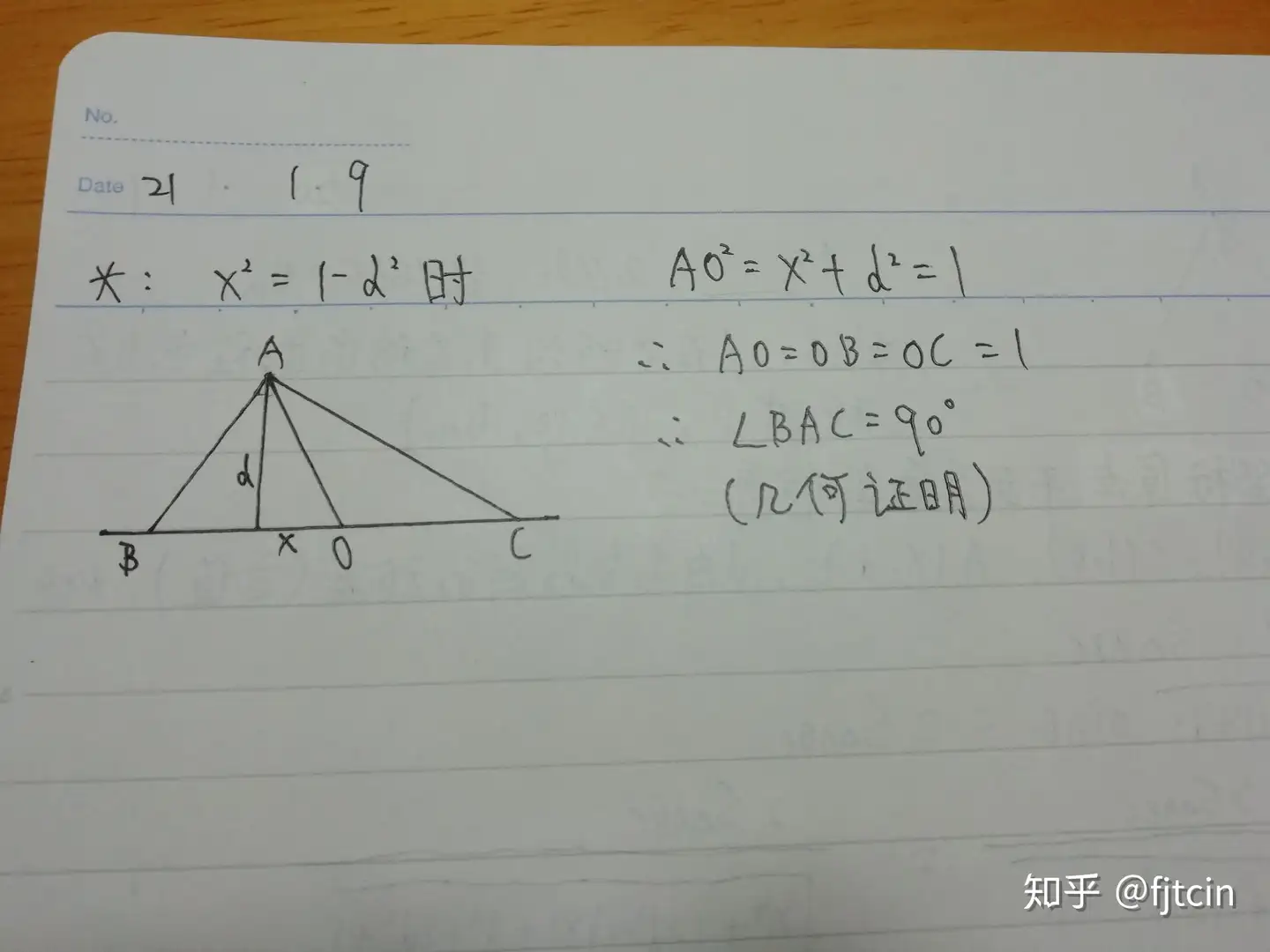 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github | 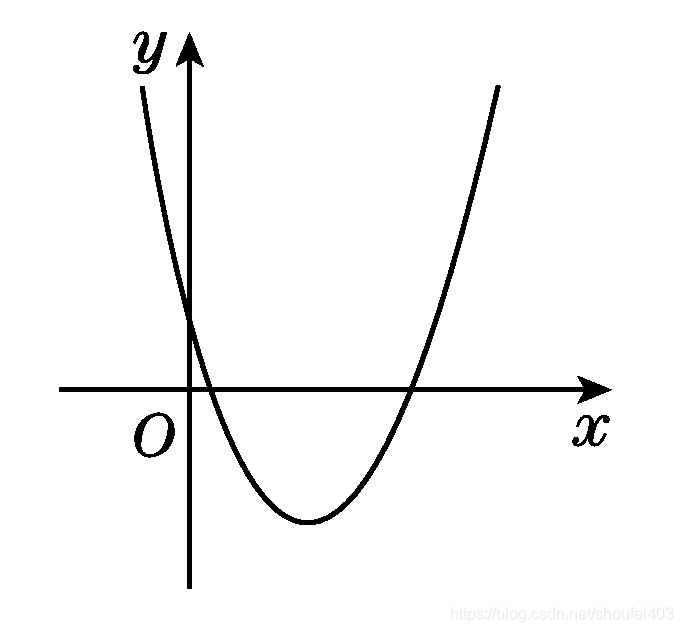 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
 Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |  Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
Acm Icpc Readme Md At Master Neu Testaccount Acm Icpc Github |
2次不等式(にじふとうしき)とは、左辺が2次式からなる不等式です。 ax 2 bxc>0やax 2 bxc<0が2次不等式です。 2次不等式の解を求めることで、xの範囲がわかります。 今回は2次不等式の問題 下記の不等式を解いてください。 1x3 > 4x8 1x-4x > -38 -3x > 5 x < -5/3 です。 まとめ 今回は不等式について説明しました。意味や解き方、性質など理解頂けたと
Incoming Term: 不等式 問題, 不等式 問題 中学, 不等式 問題 難しい, 不等式 問題 プリント, 不等式 問題文, 不等式 問題 中一, 不等式 問題 解き方, 不等式 問題 答え, 不等式 問題 作り方, 不等式 問題 絶対値,




0 件のコメント:
コメントを投稿